Brussels Sprout Production in the United States
Nov 20, 2018
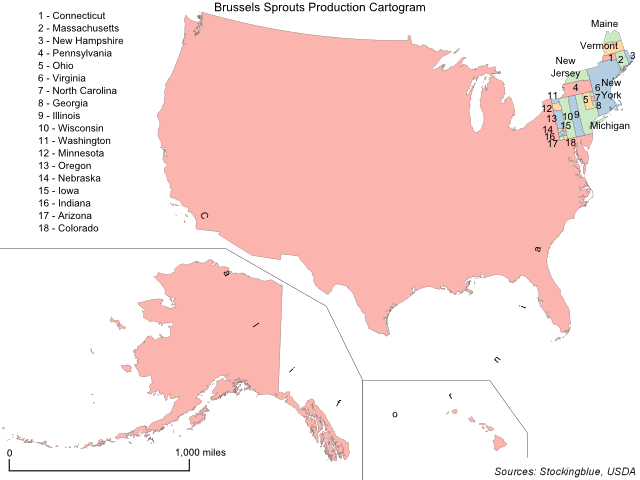
This week, like last year, the focus is on common Thanksgiving foods and which states produce them. The geographically accurate cartogram above redraws the states' sizes based on Brussels sprout production. Specifically the number of acres harvested. Only 32 states produce the vegetable and of the 32, the USDA publishes complete data on only 24 of them due to the other eight states either having few producers which would make it easy for their competitors to know how large their operations are or a very small number of acres harvested.